Functions
A function $f$ from a set $X$ to a set $Y$ is an assignment (denoted as $f:X \rightarrow Y$) that assigns to each element $x \in X$ exactly one element $y \in Y$ (denoted by $f(x)$). Here, $X$ is called domain of $f$ and $Y$ is called the codomain of $f$. The range of $f$ is $\{y \in Y: \exists x \in X, f(x)=y\}$. Following are examples of functions.
- $f:\{1,2,3\}\rightarrow \{a,b,c\}$ with $f(1)=c$, $f(2)=a$, $f(3)=a$
- $g:\mathbb{N} \rightarrow \mathbb{N}$ with $g(n)=n+1$ for each $n \in \mathbb{N}$
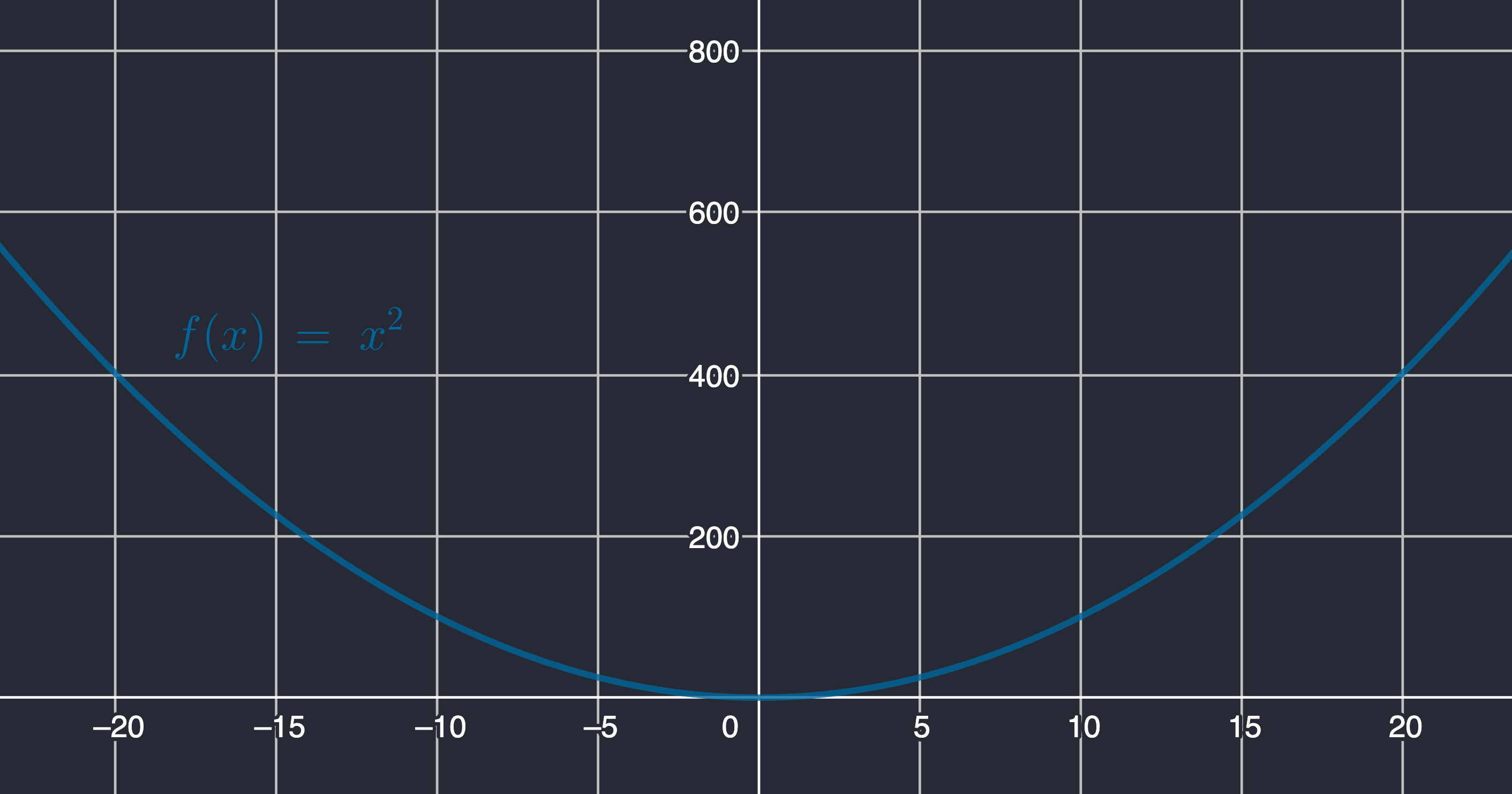
- $h:\mathbb{R} \rightarrow \mathbb{R}$ with $h(x)=x^2$ for each $x \in \mathbb{R}$

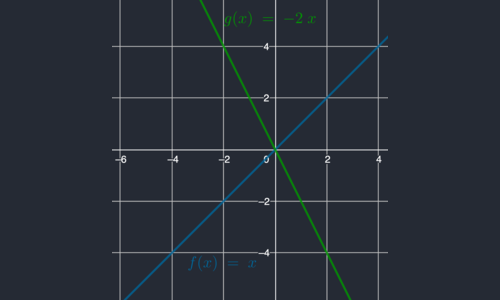
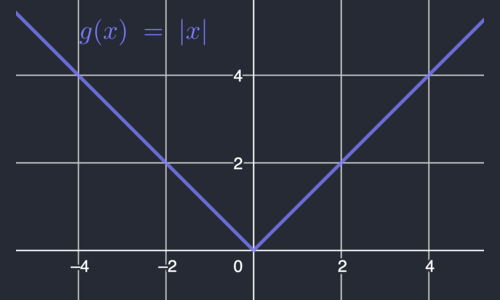
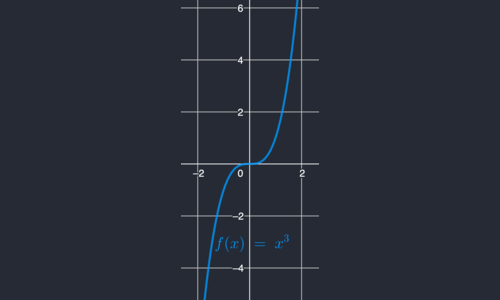
Examples of Real Functions
Composition of Functions
For functions $f:\mathbb{R}\rightarrow \mathbb{R}$ and $g:\mathbb{R}\rightarrow \mathbb{R}$, define a new function $g \circ f:\mathbb{R} \rightarrow \mathbb{R}$ as $(g \circ f)(x)=g(f(x))$. View $(g \circ f)(x)$ as the function $g$ applied after applying $f$ to $x$. Sophisticated functions can be built from simpler functions using compositions.
To learn more, check out the Slides and the Worksheet for this session!